Почему кратчайшим расстоянием в океане является не прямая, а кривая?

Изображение на бумаге частей земной поверхности – дело непростое даже в принципе, потому что Земля – шар, а известно, что никакую часть шаровой поверхности нельзя развернуть на плоскости без складок и разрывов. Поневоле приходится мириться с неизбежными искажениями на картах. Придумано много способов черчения карт, но все карты не свободны от недостатков: на одних имеются искажения одного рода, на других иного рода, но карт вовсе без искажений нет.

На морской карте кратчайший путь от мыса Доброй Надежды до южной оконечности Австралии обозначается не прямой линией («локсодромией»), а кривой («ортодромией»)

Моряки пользуются картами, начерченными по способу старинного голландского картографа и математика XVI в. Меркатора. Способ этот называется «меркаторской проекцией». Узнать морскую карту легко по ее прямоугольной сетке: меридианы изображены на ней в виде ряда параллельных прямых линий; круги широты – тоже прямыми линиями, перпендикулярными к первым.
Допустим, требуется найти кратчайший путь от одного океанского порта до другого, лежащего на той же параллели. На океане все пути доступны, и осуществить там путешествие по кратчайшему пути всегда возможно, если знать, как он пролегает. В нашем случае естественно думать, что кратчайший путь идет вдоль той параллели, на которой лежат оба порта: ведь на карте – это прямая линия, а что может быть короче прямого пути! Но мы ошибаемся: путь по параллели вовсе не кратчайший.

Криволинейный путь, соединяющий на морской карте Иокогаму с Панамским каналом, короче прямой линии, проведенной между теми же точками.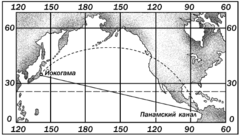

В самом деле: на поверхности шара кратчайшее расстояние между двумя точками есть соединяющая их дуга большого круга. Большим кругом на поверхности шара называется всякий круг, центр которого совпадает с центром этого шара. Все остальные круги на шаре называются малыми.
Но круг параллели – малый круг. Дуга большого круга менее искривлена, чем дуга любого малого круга, проведенного через те же две точки: большему радиусу отвечает меньшая кривизна. Натянув на глобусе нить между нашими двумя точками, вы убедитесь, что она вовсе не ляжет вдоль параллели. Натянутая нить – бесспорный указатель кратчайшего пути, а если она на глобусе не совпадает с параллелью, то и на морской карте кратчайший путь не обозначается прямой линией: вспомним, что круги параллелей изображаются на такой карте прямыми линиями, всякая же линия, не совпадающая с прямой, есть кривая.

Я.И. Перельман «Занимательная астрономия»

http://www.geoadvice.ru/index.php?option=com_content&view=article&id=65:2010-11-05-08-37-54&catid=18:2010-11-05-07-26-50&Itemid=24
Вот здесь об этом. Копировать много слишком.

ДА все же очевииидно!)))МОрякам что делать пока плывут?Пить!)))Следовательно и кораболь покачивает по курсу))))

что за бред